2. BÖLÜM : Geometrik Çizimler
- 1 GEOMETRİK ŞEKİLLER
- 2 DOĞRULARLA İLGİLİ ÇİZİMLER
- 3 AÇILARLA İLGİLİ ÇİZİMLER
- 4 DAİRE İÇİNE ÜÇGEN, DÖRTGEN, BEŞGEN ve ALTIGEN ÇİZİMİ
- 5 DAİRE İÇİNE YEDİGEN, SEKİZGEN, DOKUZGEN ve ONGEN ÇİZİMİ
- 6 GENEL METOTLA ve DİĞER METOTLARLA ÇOKGEN ÇİZİMLERİ
- 7 DAİRELERE TEĞET DOĞRU ÇİZİMLERİ-1
- 8 DAİRELERE TEĞET DOĞRU ÇİZİMLERİ-2
- 9 ÜÇGEN, DAİRE ve YAY İŞLEMLERİ
- 10 OBJELERİ TEĞET YAYLA BİRLEŞTİRME-1
- 11 OBJELERİ TEĞET YAYLA BİRLEŞTİRME-2
- 12 ELİPS ÇİZİMLERİ
- 13 OVAL ÇİZİMLERİ
- 14 PARABOL ÇİZİMLERİ
- 15 SPİRAL ÇİZİMLERİ
- 16 EVOLVENT ve SİKLOİT EĞRİLERİ
- 17 EPİSİKLOİT,HİPOSİKLOİT ve HELİS EĞRİLERİ
EPİSİKLOİT,HİPOSİKLOİT ve HELİS EĞRİLERİ
1. “EPİSİKLOİT EĞRİSİ” ÇİZMEK
Bir daire, başka bir daire üzerinde kaymadan yuvarlandığında, daire üzerindeki bir noktanın çizdiği eğriye episikloit eğrisi denir. Episikloit eğrisi de dişli çarklarda diş profillerinin çizimi ve yapımında kullanılır. Burada iki daire kullanılmaktadır. Bu daireleri büyük ve küçük çaplı iki dişli çark olarak kabul edebiliriz.
Episikloit eğrisini çizmek için sikloit eğrinin çiziminde uygulan çizim metodu aynen uygulanır. Burada paralel doğrular üzerinde yuvarlanılan dairenin çemberine paralel alınır.
Episikloid eğrisi çizmek için aşağıdaki işlem sırası uygulanır:
1. Yarı çapı 50 mm verilen daire çizilir. Dairenin çevresi eşit sayılara bölünür ve numaralandırılır. Biz 8 eşit parçaya böldük.
2. Yarı çapı 50 mm olan daire, yarıçapı 150 mm olan diğer daire üzerinde dönecektir. Dönen direnin çevre uzunluğundaki bir yayı, büyük daire üzerine işaretlememiz gerekmektedir. Bunu sağlamak için aşağıdaki işlemler yapılır:
a. Dönen küçük dairenin çevresi uzunluğu hesaplanır.
Ç1= 2xπxr = 2x3,14x50 = 314 mm bulunur.
b. Büyük dairenin çevre uzunluğu hesaplanır.
Ç2= 2xπxr = 2x3,14x150 = 942 mm bulunur.
c. Küçük dairenin çevre uzunluğu, büyük daire üzerine serildiğinde kaç derecelik açıya denk geldiğini bulmak için doğru orantı hesabı kullanılır.
942 mm uzunluk 360 dereceye karşılık gelirse, 314 mm uzunluk kaç derece açıya karşılık gelir. X=314x360/942=120 derece açı bulunur.
d. Bu hesaba göre büyük daire üzerinde 120 derecelik açıdaki yay parçası kullanılacak. İki bölüntü arasındaki merkezi açıyı bulmak için 120/8=15 derece bulunur.
3. Şekil 1’ de görüldüğü gibi büyük daire üzerinde 120 derecelik açıdaki yay işaretlenir. Bu açı 8’ e bölündüğünde 15 derece bulunur. 120 derecelik yay parçası 15 derecelik açılara bölünür. Bölüntüler merkezle birleştirir ve aynı doğrultuda uzatılır. Bölüntüler 0’ dan başlanarak numaralandırılır.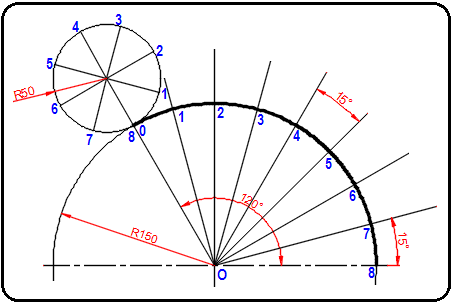
Şekil 1:Daireler üzerindeki bölüntüler 4. Şekil 2’ de görüldüğü gibi büyük dairenin üzerindeki O noktası merkez alınarak küçük daire üzerindeki bölüntülerden yaylar çizilir. Küçük dairenin merkezinden çizilen yaya kadar büyük daire üzerindeki bölüntü doğruları uzatılarak O1, O2 … merkez noktaları işaretlenir.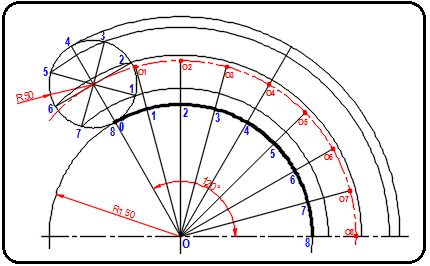
Şekil 2:Yaylar ve merkezler 5. Pergel yarıçap kadar açılır.
O1 noktası merkez alınarak 1 numaralı yay kestirilir ve A harfiyle harflendirilir. Burada resim karışmasın diye daireler tam çizilmemiştir.
O2 noktası merkez alınarak 2 numaralı yay kestirilir ve B harfiyle harflendirilir.
O3 noktası merkez alınarak 3 numaralı yay kestirilir ve C harfiyle harflendirilir.
O4 noktası merkez alınarak 4 numaralı yay kestirilir ve D harfiyle harflendirilir.
O5 noktası merkez alınarak 5 numaralı yay kestirilir ve E harfiyle harflendirilir.
O6 noktası merkez alınarak 6 numaralı yay kestirilir ve F harfiyle harflendirilir.
O7 noktası merkez alınarak 7 numaralı yay kestirilir ve G harfiyle harflendirilir.
O8 noktası merkez alınarak 8 numaralı yay kestirilir ve H harfiyle harflendirilir ve episikloid eğrisinin geçeceği noktalar bulunmuştur (Şekil 3).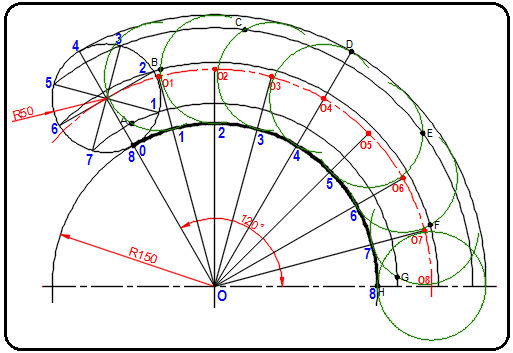
Şekil 3:Episikloid doğrusunun geçeceği noktalar 6. 0’ dan başlayarak A, B…H harfleriyle belirtilen noktalar pistole eğri cetveliyle üçer üçer hizalanarak episikloit eğrisi çizilir (Şekil 4).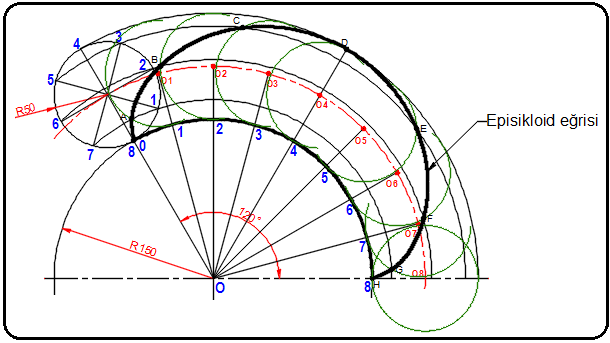
Şekil 4:Episikloid eğrisi çizimi 2. “HİPOSİKLOİT EĞRİSİ” ÇİZMEK
Bir daire, başka bir daire içinde kaymadan yuvarlandığında, daire üzerindeki bir noktanın çizdiği eğriye hiposikloit eğrisi denir. Hiposikloit eğrileri de dişli çarklarda diş profillerinin çizimi ve yapımında kullanılır. Burada iki daire kullanılmaktadır. Bu daireleri büyük ve küçük çaplı iki dişli çark olarak kabul edebiliriz. Küçük çaplı dişli büyük çaplı dişlinin içinde çalışmaktedır.
Hiposikloit eğrisinin hesapları ve çizimi için episikloit ve sikloit eğrilerinin çiziminde uygulan çizim metodu aynen uygulanır. Şekil 5’ de hiposikloit eğrisi görülmektedir.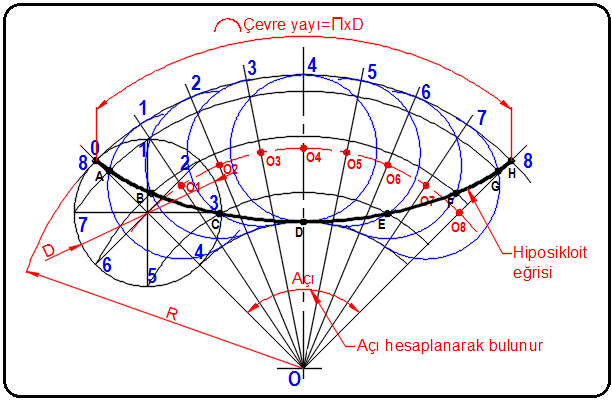
Şekil 5:Episikloit eğrisi çizimi 3. “HELİS EĞRİSİ” ÇİZMEK
Sabit hızla kendi ekseni etrafında dönen bir silindirin üzerinde, silindir ekseni doğrultusunda sabit hızla ilerleyen bir noktanın çizdiği eğriye helis denir.
Başka bir tanımlamayla, bir dik üçgen bir silindirin çevresine sarıldığında hipotenüsün aldığı şekle helis denir.
Helis eğrisinin bir dönüşteki yükselme miktarına adım denir. Helis eğrisi dişli çarklarda, vidalarda kullanılır.
Bir silindirin üzerine adımı 80 mm olan helis eğrisi çizmek için aşağıdaki işlem sırası uygulanır: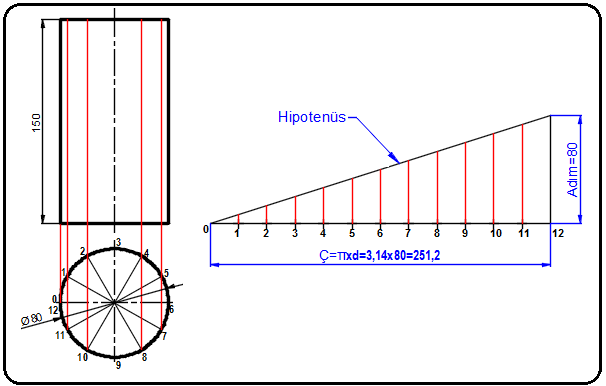
Şekil 6:Görünüşler ve bölüntü 1. Ön ve üst görünüşler çizilir. Üst görünüş olan daire istenildiği kadar eşit sayıya bölünür. Burada 12 eşit parçaya bölünmüştür.
2. Görünüşlerin hemen sağ tarafına ve ön görünüşün taban hizasında dik bir üçgen çizilir. Üçgenin taban kenarının uzunluğu silindirin taban dairesinin çevre uzunluğuna eşit alınır. Üçgenin diğer dik kenar uzunluğu ise adıma eşit alınır. Üçgenin taban kenarı da 12 eşit parçaya bölünür ve numaralandırılır. Bölüntü noktalarından hipotenüse kadar dik doğrular çizilir (Şekil 6).
3. Hipotenüs üzerindeki numaralı noktalar, silindirin ön görünüşündeki aynı numaralı bölüntü çizgileriyle kestirilir (Şekil 7).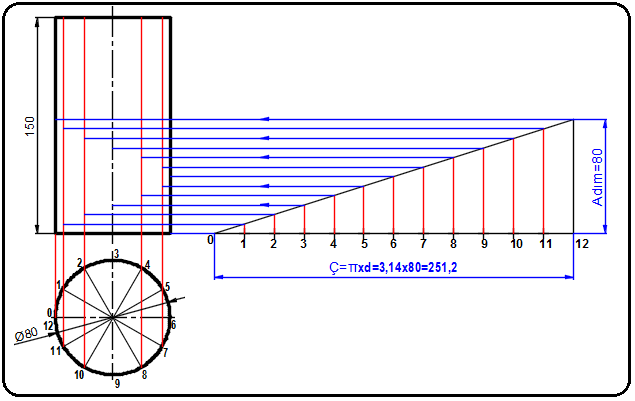
Şekil 7:Bölüntülerin taşınması ve birbiriyle kestirilmesi 4. Silindirin ön görünüşündeki 0-6 numaralı noktalar görünür, 6-12 numaralı noktalar arkada kaldığı için görünmezler. Pistoleyle görünen noktalar sürekli kalın eğri çizgiyle, görünmeyen noktalar ince kesik eğri çizgiyle birleştirilirler (Şekil 8).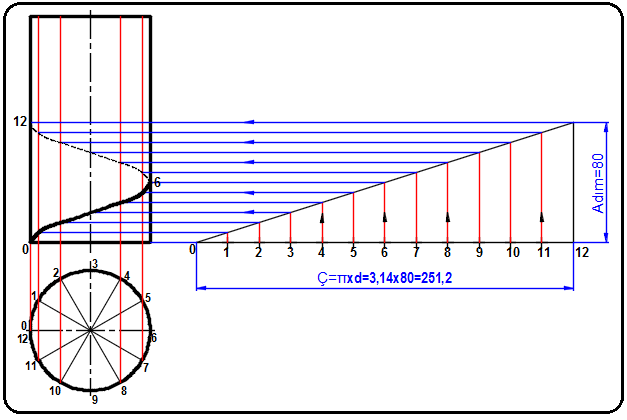
Şekil 8:Helis eğrisinin oluşturulması
Bir daire, başka bir daire üzerinde kaymadan yuvarlandığında, daire üzerindeki bir noktanın çizdiği eğriye episikloit eğrisi denir. Episikloit eğrisi de dişli çarklarda diş profillerinin çizimi ve yapımında kullanılır. Burada iki daire kullanılmaktadır. Bu daireleri büyük ve küçük çaplı iki dişli çark olarak kabul edebiliriz.
Episikloit eğrisini çizmek için sikloit eğrinin çiziminde uygulan çizim metodu aynen uygulanır. Burada paralel doğrular üzerinde yuvarlanılan dairenin çemberine paralel alınır.
Episikloid eğrisi çizmek için aşağıdaki işlem sırası uygulanır:
1. Yarı çapı 50 mm verilen daire çizilir. Dairenin çevresi eşit sayılara bölünür ve numaralandırılır. Biz 8 eşit parçaya böldük.
2. Yarı çapı 50 mm olan daire, yarıçapı 150 mm olan diğer daire üzerinde dönecektir. Dönen direnin çevre uzunluğundaki bir yayı, büyük daire üzerine işaretlememiz gerekmektedir. Bunu sağlamak için aşağıdaki işlemler yapılır:
a. Dönen küçük dairenin çevresi uzunluğu hesaplanır.
Ç1= 2xπxr = 2x3,14x50 = 314 mm bulunur.
b. Büyük dairenin çevre uzunluğu hesaplanır.
Ç2= 2xπxr = 2x3,14x150 = 942 mm bulunur.
c. Küçük dairenin çevre uzunluğu, büyük daire üzerine serildiğinde kaç derecelik açıya denk geldiğini bulmak için doğru orantı hesabı kullanılır.
942 mm uzunluk 360 dereceye karşılık gelirse, 314 mm uzunluk kaç derece açıya karşılık gelir. X=314x360/942=120 derece açı bulunur.
d. Bu hesaba göre büyük daire üzerinde 120 derecelik açıdaki yay parçası kullanılacak. İki bölüntü arasındaki merkezi açıyı bulmak için 120/8=15 derece bulunur.
3. Şekil 1’ de görüldüğü gibi büyük daire üzerinde 120 derecelik açıdaki yay işaretlenir. Bu açı 8’ e bölündüğünde 15 derece bulunur. 120 derecelik yay parçası 15 derecelik açılara bölünür. Bölüntüler merkezle birleştirir ve aynı doğrultuda uzatılır. Bölüntüler 0’ dan başlanarak numaralandırılır.

Şekil 1:Daireler üzerindeki bölüntüler 4. Şekil 2’ de görüldüğü gibi büyük dairenin üzerindeki O noktası merkez alınarak küçük daire üzerindeki bölüntülerden yaylar çizilir. Küçük dairenin merkezinden çizilen yaya kadar büyük daire üzerindeki bölüntü doğruları uzatılarak O1, O2 … merkez noktaları işaretlenir.

Şekil 2:Yaylar ve merkezler 5. Pergel yarıçap kadar açılır.
O1 noktası merkez alınarak 1 numaralı yay kestirilir ve A harfiyle harflendirilir. Burada resim karışmasın diye daireler tam çizilmemiştir.
O2 noktası merkez alınarak 2 numaralı yay kestirilir ve B harfiyle harflendirilir.
O3 noktası merkez alınarak 3 numaralı yay kestirilir ve C harfiyle harflendirilir.
O4 noktası merkez alınarak 4 numaralı yay kestirilir ve D harfiyle harflendirilir.
O5 noktası merkez alınarak 5 numaralı yay kestirilir ve E harfiyle harflendirilir.
O6 noktası merkez alınarak 6 numaralı yay kestirilir ve F harfiyle harflendirilir.
O7 noktası merkez alınarak 7 numaralı yay kestirilir ve G harfiyle harflendirilir.
O8 noktası merkez alınarak 8 numaralı yay kestirilir ve H harfiyle harflendirilir ve episikloid eğrisinin geçeceği noktalar bulunmuştur (Şekil 3).

Şekil 3:Episikloid doğrusunun geçeceği noktalar 6. 0’ dan başlayarak A, B…H harfleriyle belirtilen noktalar pistole eğri cetveliyle üçer üçer hizalanarak episikloit eğrisi çizilir (Şekil 4).

Şekil 4:Episikloid eğrisi çizimi 2. “HİPOSİKLOİT EĞRİSİ” ÇİZMEK
Bir daire, başka bir daire içinde kaymadan yuvarlandığında, daire üzerindeki bir noktanın çizdiği eğriye hiposikloit eğrisi denir. Hiposikloit eğrileri de dişli çarklarda diş profillerinin çizimi ve yapımında kullanılır. Burada iki daire kullanılmaktadır. Bu daireleri büyük ve küçük çaplı iki dişli çark olarak kabul edebiliriz. Küçük çaplı dişli büyük çaplı dişlinin içinde çalışmaktedır.
Hiposikloit eğrisinin hesapları ve çizimi için episikloit ve sikloit eğrilerinin çiziminde uygulan çizim metodu aynen uygulanır. Şekil 5’ de hiposikloit eğrisi görülmektedir.

Şekil 5:Episikloit eğrisi çizimi 3. “HELİS EĞRİSİ” ÇİZMEK
Sabit hızla kendi ekseni etrafında dönen bir silindirin üzerinde, silindir ekseni doğrultusunda sabit hızla ilerleyen bir noktanın çizdiği eğriye helis denir.
Başka bir tanımlamayla, bir dik üçgen bir silindirin çevresine sarıldığında hipotenüsün aldığı şekle helis denir.
Helis eğrisinin bir dönüşteki yükselme miktarına adım denir. Helis eğrisi dişli çarklarda, vidalarda kullanılır.
Bir silindirin üzerine adımı 80 mm olan helis eğrisi çizmek için aşağıdaki işlem sırası uygulanır:

Şekil 6:Görünüşler ve bölüntü 1. Ön ve üst görünüşler çizilir. Üst görünüş olan daire istenildiği kadar eşit sayıya bölünür. Burada 12 eşit parçaya bölünmüştür.
2. Görünüşlerin hemen sağ tarafına ve ön görünüşün taban hizasında dik bir üçgen çizilir. Üçgenin taban kenarının uzunluğu silindirin taban dairesinin çevre uzunluğuna eşit alınır. Üçgenin diğer dik kenar uzunluğu ise adıma eşit alınır. Üçgenin taban kenarı da 12 eşit parçaya bölünür ve numaralandırılır. Bölüntü noktalarından hipotenüse kadar dik doğrular çizilir (Şekil 6).
3. Hipotenüs üzerindeki numaralı noktalar, silindirin ön görünüşündeki aynı numaralı bölüntü çizgileriyle kestirilir (Şekil 7).

Şekil 7:Bölüntülerin taşınması ve birbiriyle kestirilmesi 4. Silindirin ön görünüşündeki 0-6 numaralı noktalar görünür, 6-12 numaralı noktalar arkada kaldığı için görünmezler. Pistoleyle görünen noktalar sürekli kalın eğri çizgiyle, görünmeyen noktalar ince kesik eğri çizgiyle birleştirilirler (Şekil 8).

Şekil 8:Helis eğrisinin oluşturulması



